Stock Price Prediction of Apple with PyTorch
LSTM and GRU
Time Series
Machine Learning’s captivating domain of time series forecasting commands attention, offering potentially significant benefits when integrated with advanced subjects like stock price prediction. Essentially, time series forecasting employs a specific model to anticipate future data points by utilizing the patterns found in previously observed value.
A time series, by definition, is a sequence of data points arranged in chronological order. This kind of problem holds significant relevance because numerous prediction challenges incorporate a temporal aspect. Uncovering the relationship between data and time is crucial to these analyses, such as weather forecasting or earthquake prediction. However, these issues are occasionally overlooked due to the non-trivial complexities involved in modeling these temporal relationships.
Stock market prediction entails efforts to estimate the future value of a company’s stock. The accurate prognostication of a stock’s future price can result in substantial gains, fitting this scenario into the realm of time series problems.
Over time, numerous methods have been developed to predict stock prices accurately, given their volatile and complex fluctuations. Neural networks, particularly Recurrent Neural Networks (RNNs), have exhibited significant applicability in this field. In this context, we will construct two distinct RNN models — Long Short-Term Memory (LSTM) and Gated Recurrent Units (GRU) — using PyTorch. We aim to forecast Apples’s stock market price and compare these models’ performance in aspects of time and efficiency.
Recurrent Neural Network (RNN)
A Recurrent Neural Network (RNN) is a particular breed of artificial neural network crafted to discern patterns in sequential data to anticipate ensuing events. The power of this architecture lies in its interconnected nodes, enabling it to demonstrate dynamic behavior over time. Another notable attribute of this structure is the utilization of feedback loops for sequence processing. This feature facilitates the persistence of information, often likened to memory, rendering RNNs ideal for Natural Language Processing (NLP) and time series problems. This foundational structure gave rise to advanced architectures such as Long Short-Term Memory (LSTM) and Gated Recurrent Units (GRU).
An LSTM unit comprises a cell and three gates: an input gate, an output gate, and a forget gate. The cell retains values over arbitrary time intervals, while the trio of gates control the influx and efflux of information from the cell.
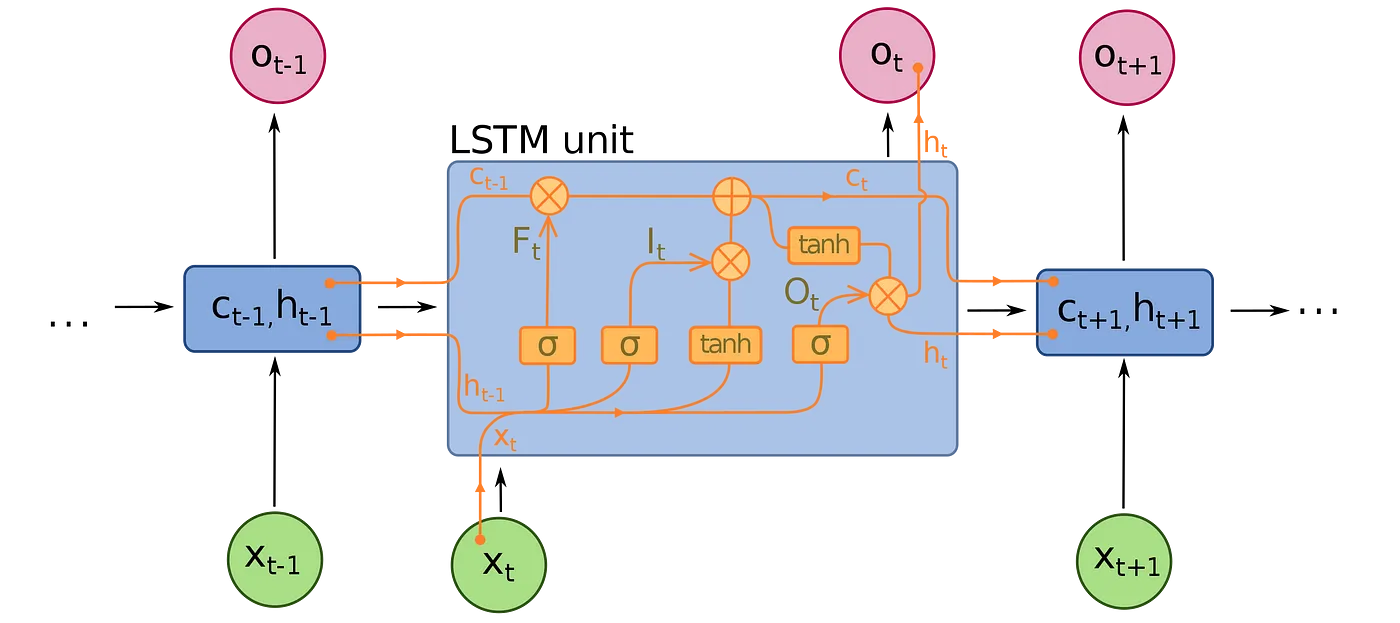
Conversely, a GRU possesses fewer parameters compared to an LSTM as it lacks an output gate. However, both configurations are capable of resolving the “short-term memory” problem typically associated with basic RNNs, and successfully maintain long-term correlations in sequential data.
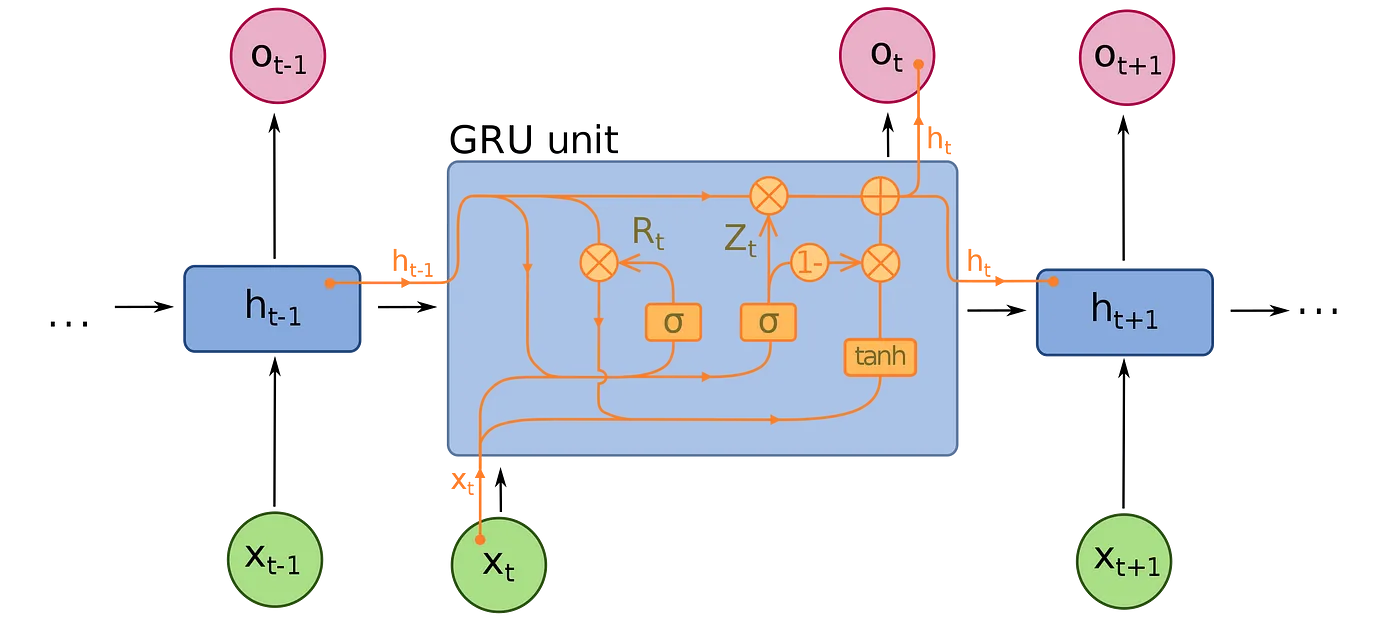
While LSTM enjoys greater popularity at present, it’s anticipated that GRU will ultimately surpass it due to its enhanced speed while maintaining comparable accuracy and effectiveness. It’s likely that we’ll observe a similar outcome in this case, with the GRU model demonstrating superior performance under these conditions.
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the read-only "../input/" directory
# For example, running this (by clicking run or pressing Shift+Enter) will list all files under the input directory
import os
for dirname, _, filenames in os.walk('./archive'):
for filename in filenames:
print(os.path.join(dirname, filename))
./archive/JPM_2006-01-01_to_2018-01-01.csv
./archive/MSFT_2006-01-01_to_2018-01-01.csv
./archive/JNJ_2006-01-01_to_2018-01-01.csv
./archive/UNH_2006-01-01_to_2018-01-01.csv
./archive/CAT_2006-01-01_to_2018-01-01.csv
./archive/AABA_2006-01-01_to_2018-01-01.csv
./archive/HD_2006-01-01_to_2018-01-01.csv
./archive/CVX_2006-01-01_to_2018-01-01.csv
./archive/MMM_2006-01-01_to_2018-01-01.csv
./archive/AMZN_2006-01-01_to_2018-01-01.csv
./archive/CSCO_2006-01-01_to_2018-01-01.csv
./archive/XOM_2006-01-01_to_2018-01-01.csv
./archive/all_stocks_2017-01-01_to_2018-01-01.csv
./archive/VZ_2006-01-01_to_2018-01-01.csv
./archive/WMT_2006-01-01_to_2018-01-01.csv
./archive/GS_2006-01-01_to_2018-01-01.csv
./archive/AAPL_2006-01-01_to_2018-01-01.csv
./archive/AXP_2006-01-01_to_2018-01-01.csv
./archive/all_stocks_2006-01-01_to_2018-01-01.csv
./archive/GOOGL_2006-01-01_to_2018-01-01.csv
./archive/UTX_2006-01-01_to_2018-01-01.csv
./archive/KO_2006-01-01_to_2018-01-01.csv
./archive/MRK_2006-01-01_to_2018-01-01.csv
./archive/TRV_2006-01-01_to_2018-01-01.csv
./archive/IBM_2006-01-01_to_2018-01-01.csv
./archive/INTC_2006-01-01_to_2018-01-01.csv
./archive/PFE_2006-01-01_to_2018-01-01.csv
./archive/GE_2006-01-01_to_2018-01-01.csv
./archive/DIS_2006-01-01_to_2018-01-01.csv
./archive/PG_2006-01-01_to_2018-01-01.csv
./archive/BA_2006-01-01_to_2018-01-01.csv
./archive/MCD_2006-01-01_to_2018-01-01.csv
./archive/NKE_2006-01-01_to_2018-01-01.csv
Implementation
The dataset contains historical stock prices. We are going to predict the Close price of the stock, and the following is the data behavior over the years.
filepath = './archive/AAPL_2006-01-01_to_2018-01-01.csv'
data = pd.read_csv(filepath)
data = data.sort_values('Date')
data.head()
| Date | Open | High | Low | Close | Volume | Name | |
|---|---|---|---|---|---|---|---|
| 0 | 2006-01-03 | 10.34 | 10.68 | 10.32 | 10.68 | 201853036 | AAPL |
| 1 | 2006-01-04 | 10.73 | 10.85 | 10.64 | 10.71 | 155225609 | AAPL |
| 2 | 2006-01-05 | 10.69 | 10.70 | 10.54 | 10.63 | 112396081 | AAPL |
| 3 | 2006-01-06 | 10.75 | 10.96 | 10.65 | 10.90 | 176139334 | AAPL |
| 4 | 2006-01-09 | 10.96 | 11.03 | 10.82 | 10.86 | 168861224 | AAPL |

import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style("darkgrid")
plt.figure(figsize = (15,9))
plt.plot(data[['Close']])
plt.xticks(range(0,data.shape[0],500),data['Date'].loc[::500],rotation=45)
plt.title("Apple Stock Price",fontsize=18, fontweight='bold')
plt.xlabel('Date',fontsize=18)
plt.ylabel('Close Price (USD)',fontsize=18)
plt.show()
price = data[['Close']]
price.info()
<class 'pandas.core.frame.DataFrame'>
Int64Index: 3019 entries, 0 to 3018
Data columns (total 1 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Close 3019 non-null float64
dtypes: float64(1)
memory usage: 47.2 KB
I slice the data frame to get the column we want and normalize the data.
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler(feature_range=(-1, 1))
price['Close'] = scaler.fit_transform(price['Close'].values.reshape(-1,1))
/var/folders/8_/k8h_gshs3_qdkr8glv1ff08h0000gn/T/ipykernel_43516/68737012.py:4: SettingWithCopyWarning:
A value is trying to be set on a copy of a slice from a DataFrame.
Try using .loc[row_indexer,col_indexer] = value instead
See the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
price['Close'] = scaler.fit_transform(price['Close'].values.reshape(-1,1))
We’re now ready to partition the data into training and test sets. But prior to that, it’s necessary to determine the width of the analysis window. This technique of employing previous time steps to forecast the subsequent time step is referred to as the sliding window approach.
def split_data(stock, lookback):
data_raw = stock.to_numpy() # convert to numpy array
data = []
# create all possible sequences of length seq_len
for index in range(len(data_raw) - lookback):
data.append(data_raw[index: index + lookback])
data = np.array(data);
test_set_size = int(np.round(0.2*data.shape[0]));
train_set_size = data.shape[0] - (test_set_size);
x_train = data[:train_set_size,:-1,:]
y_train = data[:train_set_size,-1,:]
x_test = data[train_set_size:,:-1]
y_test = data[train_set_size:,-1,:]
return [x_train, y_train, x_test, y_test]
lookback = 20 # choose sequence length
x_train, y_train, x_test, y_test = split_data(price, lookback)
print('x_train.shape = ',x_train.shape)
print('y_train.shape = ',y_train.shape)
print('x_test.shape = ',x_test.shape)
print('y_test.shape = ',y_test.shape)
x_train.shape = (2399, 19, 1)
y_train.shape = (2399, 1)
x_test.shape = (600, 19, 1)
y_test.shape = (600, 1)
Next, we convert them into tensors, the foundational data structure required for constructing a model in PyTorch.
import torch
import torch.nn as nn
x_train = torch.from_numpy(x_train).type(torch.Tensor)
x_test = torch.from_numpy(x_test).type(torch.Tensor)
y_train_lstm = torch.from_numpy(y_train).type(torch.Tensor)
y_test_lstm = torch.from_numpy(y_test).type(torch.Tensor)
y_train_gru = torch.from_numpy(y_train).type(torch.Tensor)
y_test_gru = torch.from_numpy(y_test).type(torch.Tensor)
input_dim = 1
hidden_dim = 32
num_layers = 2
output_dim = 1
num_epochs = 100
LSTM
class LSTM(nn.Module):
def __init__(self, input_dim, hidden_dim, num_layers, output_dim):
super(LSTM, self).__init__()
self.hidden_dim = hidden_dim
self.num_layers = num_layers
self.lstm = nn.LSTM(input_dim, hidden_dim, num_layers, batch_first=True)
self.fc = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_dim).requires_grad_()
c0 = torch.zeros(self.num_layers, x.size(0), self.hidden_dim).requires_grad_()
out, (hn, cn) = self.lstm(x, (h0.detach(), c0.detach()))
out = self.fc(out[:, -1, :])
return out
model = LSTM(input_dim=input_dim, hidden_dim=hidden_dim, output_dim=output_dim, num_layers=num_layers)
criterion = torch.nn.MSELoss(reduction='mean')
optimiser = torch.optim.Adam(model.parameters(), lr=0.01)
import time
hist = np.zeros(num_epochs)
start_time = time.time()
lstm = []
for t in range(num_epochs):
y_train_pred = model(x_train)
loss = criterion(y_train_pred, y_train_lstm)
print("Epoch ", t, "MSE: ", loss.item())
hist[t] = loss.item()
optimiser.zero_grad()
loss.backward()
optimiser.step()
training_time = time.time()-start_time
print("Training time: {}".format(training_time))
Epoch 0 MSE: 0.25819653272628784
Epoch 1 MSE: 0.15166231989860535
Epoch 2 MSE: 0.20903076231479645
Epoch 3 MSE: 0.13991586863994598
Epoch 4 MSE: 0.1287676990032196
Epoch 5 MSE: 0.13563665747642517
Epoch 6 MSE: 0.13573406636714935
Epoch 7 MSE: 0.12434989213943481
Epoch 8 MSE: 0.1031389907002449
Epoch 9 MSE: 0.0779111385345459
Epoch 10 MSE: 0.06311900913715363
Epoch 11 MSE: 0.07091287523508072
Epoch 12 MSE: 0.052488457411527634
Epoch 13 MSE: 0.023740172386169434
Epoch 14 MSE: 0.01886197179555893
Epoch 15 MSE: 0.023339685052633286
Epoch 16 MSE: 0.017914501950144768
Epoch 17 MSE: 0.010528038255870342
Epoch 18 MSE: 0.020709635689854622
Epoch 19 MSE: 0.022142166271805763
Epoch 20 MSE: 0.00913378968834877
Epoch 21 MSE: 0.0032837125472724438
Epoch 22 MSE: 0.006005624774843454
Epoch 23 MSE: 0.009221922606229782
Epoch 24 MSE: 0.009343614801764488
Epoch 25 MSE: 0.007402882911264896
Epoch 26 MSE: 0.006014988292008638
Epoch 27 MSE: 0.006637887097895145
Epoch 28 MSE: 0.007978024892508984
Epoch 29 MSE: 0.007520338520407677
Epoch 30 MSE: 0.005026531405746937
Epoch 31 MSE: 0.002815255429595709
Epoch 32 MSE: 0.002627915469929576
Epoch 33 MSE: 0.0038487249985337257
Epoch 34 MSE: 0.004618681501597166
Epoch 35 MSE: 0.0039092665538191795
Epoch 36 MSE: 0.002484086435288191
Epoch 37 MSE: 0.0018542427569627762
Epoch 38 MSE: 0.002269477816298604
Epoch 39 MSE: 0.002432651352137327
Epoch 40 MSE: 0.0017461515963077545
Epoch 41 MSE: 0.001250344910658896
Epoch 42 MSE: 0.0016412724507972598
Epoch 43 MSE: 0.0022176974453032017
Epoch 44 MSE: 0.002139537362381816
Epoch 45 MSE: 0.0015903041930869222
Epoch 46 MSE: 0.0013555067125707865
Epoch 47 MSE: 0.0015729618025943637
Epoch 48 MSE: 0.0015560296596959233
Epoch 49 MSE: 0.0010814378038048744
Epoch 50 MSE: 0.0007583849364891648
Epoch 51 MSE: 0.0008783523226156831
Epoch 52 MSE: 0.0010345984483137727
Epoch 53 MSE: 0.0009140677284449339
Epoch 54 MSE: 0.0007315980619750917
Epoch 55 MSE: 0.0007604123093187809
Epoch 56 MSE: 0.0008461487013846636
Epoch 57 MSE: 0.0007311741355806589
Epoch 58 MSE: 0.0005497800884768367
Epoch 59 MSE: 0.0005577158881351352
Epoch 60 MSE: 0.0006879133288748562
Epoch 61 MSE: 0.0007144041010178626
Epoch 62 MSE: 0.0006207934347912669
Epoch 63 MSE: 0.0005688412929885089
Epoch 64 MSE: 0.0005930980551056564
Epoch 65 MSE: 0.0005647227517329156
Epoch 66 MSE: 0.00047004505177028477
Epoch 67 MSE: 0.0004422623314894736
Epoch 68 MSE: 0.0004969367873854935
Epoch 69 MSE: 0.0005126534379087389
Epoch 70 MSE: 0.00046223439858295023
Epoch 71 MSE: 0.00043931364780291915
Epoch 72 MSE: 0.0004609820316545665
Epoch 73 MSE: 0.00045188714284449816
Epoch 74 MSE: 0.0004201307019684464
Epoch 75 MSE: 0.00043058270239271224
Epoch 76 MSE: 0.0004576134087983519
Epoch 77 MSE: 0.0004446248640306294
Epoch 78 MSE: 0.0004175296053290367
Epoch 79 MSE: 0.00041787829832173884
Epoch 80 MSE: 0.00041931969462893903
Epoch 81 MSE: 0.0004008542455267161
Epoch 82 MSE: 0.0003951751277782023
Epoch 83 MSE: 0.0004096981429029256
Epoch 84 MSE: 0.00041126698488369584
Epoch 85 MSE: 0.0003979630710091442
Epoch 86 MSE: 0.0003955823485739529
Epoch 87 MSE: 0.0004000987682957202
Epoch 88 MSE: 0.0003947264631278813
Epoch 89 MSE: 0.00039027887396514416
Epoch 90 MSE: 0.00039583834586665034
Epoch 91 MSE: 0.00039670622209087014
Epoch 92 MSE: 0.0003883809840772301
Epoch 93 MSE: 0.00038467306876555085
Epoch 94 MSE: 0.00038626548484899104
Epoch 95 MSE: 0.00038355711149051785
Epoch 96 MSE: 0.0003808493784163147
Epoch 97 MSE: 0.00038343065534718335
Epoch 98 MSE: 0.0003837483818642795
Epoch 99 MSE: 0.00037956441519781947
Training time: 8.352406024932861
predict = pd.DataFrame(scaler.inverse_transform(y_train_pred.detach().numpy()))
original = pd.DataFrame(scaler.inverse_transform(y_train_lstm.detach().numpy()))
import seaborn as sns
sns.set_style("darkgrid")
fig = plt.figure()
fig.subplots_adjust(hspace=0.2, wspace=0.2)
plt.subplot(1, 2, 1)
ax = sns.lineplot(x = original.index, y = original[0], label="Data", color='royalblue')
ax = sns.lineplot(x = predict.index, y = predict[0], label="Training Prediction (LSTM)", color='tomato')
ax.set_title('Stock price', size = 14, fontweight='bold')
ax.set_xlabel("Days", size = 14)
ax.set_ylabel("Cost (USD)", size = 14)
ax.set_xticklabels('', size=10)
plt.subplot(1, 2, 2)
ax = sns.lineplot(data=hist, color='royalblue')
ax.set_xlabel("Epoch", size = 14)
ax.set_ylabel("Loss", size = 14)
ax.set_title("Training Loss", size = 14, fontweight='bold')
fig.set_figheight(6)
fig.set_figwidth(16)

import math, time
from sklearn.metrics import mean_squared_error
# make predictions
y_test_pred = model(x_test)
# invert predictions
y_train_pred = scaler.inverse_transform(y_train_pred.detach().numpy())
y_train = scaler.inverse_transform(y_train_lstm.detach().numpy())
y_test_pred = scaler.inverse_transform(y_test_pred.detach().numpy())
y_test = scaler.inverse_transform(y_test_lstm.detach().numpy())
# calculate root mean squared error
trainScore = math.sqrt(mean_squared_error(y_train[:,0], y_train_pred[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = math.sqrt(mean_squared_error(y_test[:,0], y_test_pred[:,0]))
print('Test Score: %.2f RMSE' % (testScore))
lstm.append(trainScore)
lstm.append(testScore)
lstm.append(training_time)
Train Score: 1.65 RMSE
Test Score: 5.56 RMSE
# shift train predictions for plotting
trainPredictPlot = np.empty_like(price)
trainPredictPlot[:, :] = np.nan
trainPredictPlot[lookback:len(y_train_pred)+lookback, :] = y_train_pred
# shift test predictions for plotting
testPredictPlot = np.empty_like(price)
testPredictPlot[:, :] = np.nan
testPredictPlot[len(y_train_pred)+lookback-1:len(price)-1, :] = y_test_pred
original = scaler.inverse_transform(price['Close'].values.reshape(-1,1))
predictions = np.append(trainPredictPlot, testPredictPlot, axis=1)
predictions = np.append(predictions, original, axis=1)
result = pd.DataFrame(predictions)
import plotly.express as px
import plotly.graph_objects as go
fig = go.Figure()
fig.add_trace(go.Scatter(go.Scatter(x=result.index, y=result[0],
mode='lines',
name='Train prediction')))
fig.add_trace(go.Scatter(x=result.index, y=result[1],
mode='lines',
name='Test prediction'))
fig.add_trace(go.Scatter(go.Scatter(x=result.index, y=result[2],
mode='lines',
name='Actual Value')))
fig.update_layout(
xaxis=dict(
showline=True,
showgrid=True,
showticklabels=False,
linecolor='white',
linewidth=2
),
yaxis=dict(
title_text='Close (USD)',
titlefont=dict(
family='Rockwell',
size=12,
color='white',
),
showline=True,
showgrid=True,
showticklabels=True,
linecolor='white',
linewidth=2,
ticks='outside',
tickfont=dict(
family='Rockwell',
size=12,
color='white',
),
),
showlegend=True,
template = 'plotly_dark'
)
annotations = []
annotations.append(dict(xref='paper', yref='paper', x=0.0, y=1.05,
xanchor='left', yanchor='bottom',
text='Results (LSTM)',
font=dict(family='Rockwell',
size=26,
color='white'),
showarrow=False))
fig.update_layout(annotations=annotations)
fig.show()

The model behaves well with the training set, and it also has solid performace with the test set. The model is probably overfitting, especially taking into consideration that the loss is minimal after the 40th epoch.
GRU
class GRU(nn.Module):
def __init__(self, input_dim, hidden_dim, num_layers, output_dim):
super(GRU, self).__init__()
self.hidden_dim = hidden_dim
self.num_layers = num_layers
self.gru = nn.GRU(input_dim, hidden_dim, num_layers, batch_first=True)
self.fc = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
h0 = torch.zeros(self.num_layers, x.size(0), self.hidden_dim).requires_grad_()
out, (hn) = self.gru(x, (h0.detach()))
out = self.fc(out[:, -1, :])
return out
model = GRU(input_dim=input_dim, hidden_dim=hidden_dim, output_dim=output_dim, num_layers=num_layers)
criterion = torch.nn.MSELoss(reduction='mean')
optimiser = torch.optim.Adam(model.parameters(), lr=0.01)
hist = np.zeros(num_epochs)
start_time = time.time()
gru = []
for t in range(num_epochs):
y_train_pred = model(x_train)
loss = criterion(y_train_pred, y_train_gru)
print("Epoch ", t, "MSE: ", loss.item())
hist[t] = loss.item()
optimiser.zero_grad()
loss.backward()
optimiser.step()
training_time = time.time()-start_time
print("Training time: {}".format(training_time))
Epoch 0 MSE: 0.3607046902179718
Epoch 1 MSE: 0.13102510571479797
Epoch 2 MSE: 0.19682788848876953
Epoch 3 MSE: 0.12917079031467438
Epoch 4 MSE: 0.075187087059021
Epoch 5 MSE: 0.07155207544565201
Epoch 6 MSE: 0.06979498267173767
Epoch 7 MSE: 0.045164529234170914
Epoch 8 MSE: 0.010227248072624207
Epoch 9 MSE: 0.007098929025232792
Epoch 10 MSE: 0.03696290776133537
Epoch 11 MSE: 0.023822534829378128
Epoch 12 MSE: 0.007158784195780754
Epoch 13 MSE: 0.011737179011106491
Epoch 14 MSE: 0.018340380862355232
Epoch 15 MSE: 0.01571972481906414
Epoch 16 MSE: 0.007737305015325546
Epoch 17 MSE: 0.0022043471690267324
Epoch 18 MSE: 0.003535511204972863
Epoch 19 MSE: 0.009062006138265133
Epoch 20 MSE: 0.011892840266227722
Epoch 21 MSE: 0.009278996847569942
Epoch 22 MSE: 0.004890399053692818
Epoch 23 MSE: 0.00290724472142756
Epoch 24 MSE: 0.0037367662880569696
Epoch 25 MSE: 0.005075107794255018
Epoch 26 MSE: 0.0048552630469202995
Epoch 27 MSE: 0.0029767893720418215
Epoch 28 MSE: 0.0011302019702270627
Epoch 29 MSE: 0.0010998218785971403
Epoch 30 MSE: 0.0027486730832606554
Epoch 31 MSE: 0.003973710350692272
Epoch 32 MSE: 0.0033208823297172785
Epoch 33 MSE: 0.001725937006995082
Epoch 34 MSE: 0.0009095442364923656
Epoch 35 MSE: 0.0012437441619113088
Epoch 36 MSE: 0.001808099914342165
Epoch 37 MSE: 0.001749989576637745
Epoch 38 MSE: 0.0011168664786964655
Epoch 39 MSE: 0.0006078396691009402
Epoch 40 MSE: 0.0007392823463305831
Epoch 41 MSE: 0.0012739860685542226
Epoch 42 MSE: 0.001527499407529831
Epoch 43 MSE: 0.0012058777501806617
Epoch 44 MSE: 0.0006985657382756472
Epoch 45 MSE: 0.0005090595805086195
Epoch 46 MSE: 0.0006709578447043896
Epoch 47 MSE: 0.0008276336011476815
Epoch 48 MSE: 0.0007188778254203498
Epoch 49 MSE: 0.00046144291991367936
Epoch 50 MSE: 0.00036167059442959726
Epoch 51 MSE: 0.0005161706358194351
Epoch 52 MSE: 0.0006932021933607757
Epoch 53 MSE: 0.0006540967733599246
Epoch 54 MSE: 0.00046293693594634533
Epoch 55 MSE: 0.0003537530137691647
Epoch 56 MSE: 0.0004015856538899243
Epoch 57 MSE: 0.0004694756935350597
Epoch 58 MSE: 0.0004315198748372495
Epoch 59 MSE: 0.00033121410524472594
Epoch 60 MSE: 0.0002968600601889193
Epoch 61 MSE: 0.00035973641206510365
Epoch 62 MSE: 0.00042053856304846704
Epoch 63 MSE: 0.00039580956217832863
Epoch 64 MSE: 0.00032569453469477594
Epoch 65 MSE: 0.000298373750410974
Epoch 66 MSE: 0.0003244410618208349
Epoch 67 MSE: 0.00034042992047034204
Epoch 68 MSE: 0.00031064936774782836
Epoch 69 MSE: 0.0002729821135289967
Epoch 70 MSE: 0.00027573812985792756
Epoch 71 MSE: 0.0003066273347940296
Epoch 72 MSE: 0.0003163278743159026
Epoch 73 MSE: 0.0002932495262939483
Epoch 74 MSE: 0.00027294218307361007
Epoch 75 MSE: 0.0002778717316687107
Epoch 76 MSE: 0.0002882281842175871
Epoch 77 MSE: 0.0002800409565679729
Epoch 78 MSE: 0.0002621126768644899
Epoch 79 MSE: 0.0002582546148914844
Epoch 80 MSE: 0.000269515992840752
Epoch 81 MSE: 0.0002754448796622455
Epoch 82 MSE: 0.0002673306444194168
Epoch 83 MSE: 0.0002585184993222356
Epoch 84 MSE: 0.0002598936844151467
Epoch 85 MSE: 0.0002639705198816955
Epoch 86 MSE: 0.00026010669535025954
Epoch 87 MSE: 0.0002519670524634421
Epoch 88 MSE: 0.0002499922120478004
Epoch 89 MSE: 0.0002542092406656593
Epoch 90 MSE: 0.0002556447288952768
Epoch 91 MSE: 0.0002515747328288853
Epoch 92 MSE: 0.0002483536081854254
Epoch 93 MSE: 0.0002494044601917267
Epoch 94 MSE: 0.0002502511197235435
Epoch 95 MSE: 0.00024729460710659623
Epoch 96 MSE: 0.00024373934138566256
Epoch 97 MSE: 0.00024349824525415897
Epoch 98 MSE: 0.000244816328631714
Epoch 99 MSE: 0.0002440418174955994
Training time: 8.153863906860352
predict = pd.DataFrame(scaler.inverse_transform(y_train_pred.detach().numpy()))
original = pd.DataFrame(scaler.inverse_transform(y_train_gru.detach().numpy()))
import seaborn as sns
sns.set_style("darkgrid")
fig = plt.figure()
fig.subplots_adjust(hspace=0.2, wspace=0.2)
plt.subplot(1, 2, 1)
ax = sns.lineplot(x = original.index, y = original[0], label="Data", color='royalblue')
ax = sns.lineplot(x = predict.index, y = predict[0], label="Training Prediction (GRU)", color='tomato')
ax.set_title('Stock price', size = 14, fontweight='bold')
ax.set_xlabel("Days", size = 14)
ax.set_ylabel("Cost (USD)", size = 14)
ax.set_xticklabels('', size=10)
plt.subplot(1, 2, 2)
ax = sns.lineplot(data=hist, color='royalblue')
ax.set_xlabel("Epoch", size = 14)
ax.set_ylabel("Loss", size = 14)
ax.set_title("Training Loss", size = 14, fontweight='bold')
fig.set_figheight(6)
fig.set_figwidth(16)

import math, time
from sklearn.metrics import mean_squared_error
# make predictions
y_test_pred = model(x_test)
# invert predictions
y_train_pred = scaler.inverse_transform(y_train_pred.detach().numpy())
y_train = scaler.inverse_transform(y_train_gru.detach().numpy())
y_test_pred = scaler.inverse_transform(y_test_pred.detach().numpy())
y_test = scaler.inverse_transform(y_test_gru.detach().numpy())
# calculate root mean squared error
trainScore = math.sqrt(mean_squared_error(y_train[:,0], y_train_pred[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = math.sqrt(mean_squared_error(y_test[:,0], y_test_pred[:,0]))
print('Test Score: %.2f RMSE' % (testScore))
gru.append(trainScore)
gru.append(testScore)
gru.append(training_time)
Train Score: 1.32 RMSE
Test Score: 4.90 RMSE
# shift train predictions for plotting
trainPredictPlot = np.empty_like(price)
trainPredictPlot[:, :] = np.nan
trainPredictPlot[lookback:len(y_train_pred)+lookback, :] = y_train_pred
# shift test predictions for plotting
testPredictPlot = np.empty_like(price)
testPredictPlot[:, :] = np.nan
testPredictPlot[len(y_train_pred)+lookback-1:len(price)-1, :] = y_test_pred
original = scaler.inverse_transform(price['Close'].values.reshape(-1,1))
predictions = np.append(trainPredictPlot, testPredictPlot, axis=1)
predictions = np.append(predictions, original, axis=1)
result = pd.DataFrame(predictions)
import plotly.express as px
import plotly.graph_objects as go
fig = go.Figure()
fig.add_trace(go.Scatter(go.Scatter(x=result.index, y=result[0],
mode='lines',
name='Train prediction')))
fig.add_trace(go.Scatter(x=result.index, y=result[1],
mode='lines',
name='Test prediction'))
fig.add_trace(go.Scatter(go.Scatter(x=result.index, y=result[2],
mode='lines',
name='Actual Value')))
fig.update_layout(
xaxis=dict(
showline=True,
showgrid=True,
showticklabels=False,
linecolor='white',
linewidth=2
),
yaxis=dict(
title_text='Close (USD)',
titlefont=dict(
family='Rockwell',
size=12,
color='white',
),
showline=True,
showgrid=True,
showticklabels=True,
linecolor='white',
linewidth=2,
ticks='outside',
tickfont=dict(
family='Rockwell',
size=12,
color='white',
),
),
showlegend=True,
template = 'plotly_dark'
)
annotations = []
annotations.append(dict(xref='paper', yref='paper', x=0.0, y=1.05,
xanchor='left', yanchor='bottom',
text='Results (GRU)',
font=dict(family='Rockwell',
size=26,
color='white'),
showarrow=False))
fig.update_layout(annotations=annotations)
fig.show()
lstm = pd.DataFrame(lstm, columns=['LSTM'])
gru = pd.DataFrame(gru, columns=['GRU'])
result = pd.concat([lstm, gru], axis=1, join='inner')
result.index = ['Train RMSE', 'Test RMSE', 'Train Time']
result
| LSTM | GRU | |
|---|---|---|
| Train RMSE | 1.648017 | 1.321451 |
| Test RMSE | 5.562765 | 4.904847 |
| Train Time | 8.352406 | 8.153864 |

Conclusion
Both models demonstrate commendable performance during the training phase, but their progress seems to plateau around the 40th epoch, indicating that the predefined 100 epochs may not be necessary.
In line with our expectations, the GRU neural network excelled over the LSTM in terms of accuracy, achieving a lower mean square error (in both training and, crucially, in the test set) and faster processing speed.